Function approximation is the core of many problems in machine learning. DeepMind's latest research combines the advantages of neural networks and random processes, and proposes a neural process model, which achieves good performance and high computational efficiency in multi-tasking.
Function approximation is at the core of many problems in machine learning. In the past decade, a very popular method for this problem is deep neural networks. Advanced neural networks consist of black box function approximators that learn to parameterize a single function from a large number of training data points. Therefore, most of the workload of the network falls in the training phase, while the evaluation and testing phases are reduced to fast forward propagation. Although high test time performance is valuable for many practical applications, the output of the network cannot be updated after training, which may be undesirable. For example, Meta-learning is an increasingly popular research field that addresses this limitation.
As an alternative to neural networks, it is also possible to reason about random processes to perform functional regression. The most common example of this method is the Gaussian process (Gaussian process, GP), which is a neural network model with complementary properties: GP does not require an expensive training phase, and can perform ground truth functions based on certain observations. Inferred, this makes them very flexible when testing.
In addition, GP represents an infinite number of different functions in unobserved positions, so given some observations, it can capture the uncertainty of its prediction. However, GP is computationally expensive: the original GP is a scale of the order of 3 to the number of data points, and the current optimal approximation method is quadratic approximation. In addition, the available kernel is usually limited in its functional form, and an additional optimization process is required to determine the most suitable kernel and its hyperparameters for any given task.
Therefore, combining neural network and stochastic process reasoning to make up for some of the shortcomings of the two methods has attracted more and more attention as a potential solution. In this work, the team of DeepMind research scientist Marta Garnelo and others proposed a method based on neural networks and learning random process approximation, which they called Neural Processes (NPs). NP has some basic properties of GP, that is, they learn to model the distribution on the function, can estimate the uncertainty of their prediction based on the observation of the context, and transfer some work from training to testing time to achieve model flexibility.
More importantly, NP generates predictions in a very computationally efficient way. Given n context points and m target points, a trained NP inference corresponds to the forward pass of a deep neural network, which is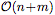 
scale, instead of using 
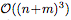. In addition, the model overcomes many functional design limitations by directly learning implicit kernels from data.
The main contributions of this research are:
Propose Neural Processes, which is a model that combines the advantages of neural networks and random processes.
We compared neural processes (NP) with meta-learning, deep latent variable models, and Gaussian processes. Given how relevant NPs are to these areas, they allow comparisons between many related topics.
We have demonstrated the advantages and capabilities of NP by applying NP to a series of tasks, including one-dimensional regression, true image completion, Bayesian optimization, and contextual bandits.
Neural process model
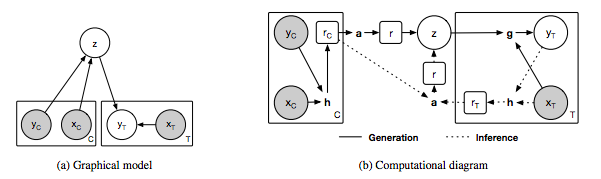
Figure 1: Neural process model.
(A) The graph model of neural process, x and y respectively correspond to the data of y = f(x), C and T respectively represent the number of context points and target points, and z represents the global latent variable. The gray background indicates that the variable is observed.
(B) Schematic diagram of the realization of neural process. The variables in the circle correspond to the variables of the graph model in (a). The variables in the box represent the middle representation of NP, and the bold letters represent the following calculation modules: h-encoder, a-aggregator and g-decoder. In our implementation, h and g correspond to the neural network, and a corresponds to the mean function. The solid line represents the generation process, and the dashed line represents the inference process.
In our NP implementation, we provide two additional requirements: the order of context points and the invariance of computational efficiency.
The final model can be boiled down to the following three core components (see Figure 1b):
From the input space to the encoder h representing the space, the input is paired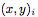 
Context value and generate a representation for each pair 
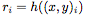. We parameterize h as a neural network.
Aggregator a, which summarizes the input of the encoder.
Conditional decoder (conditional decoder) g, it will sample the global latent variable z and the new target position 
As input and for the corresponding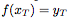 
Output prediction 
.
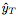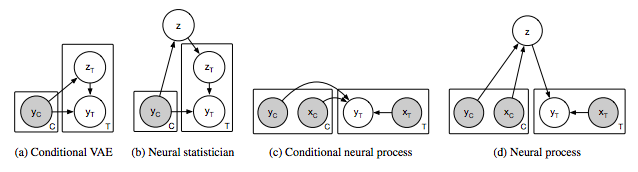
Figure 2: Graphical model of correlation model (ac) and neural process (d). Gray shading indicates the observed variable. C represents the context variable, and T represents the target variable, that is, the variable to be predicted when C is given.
result
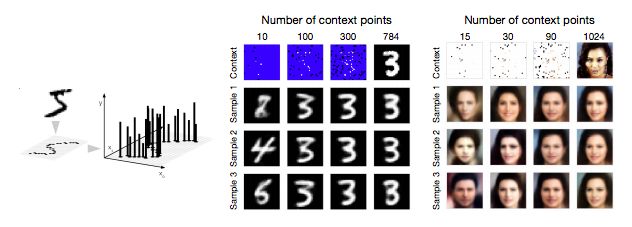
Figure 4. Pixelated regression on MNIST and CelebA
The figure on the left shows that an image that is pixelated can be framed as a 2-D regression task, where f (pixel coordinates) = pixel brightness. The figure on the right shows the results of the image implementation of MNIST and CelebA. The top image corresponds to the context node provided to the model. In order to show more clearly, unobserved points are marked as blue and white in MNIST and CelebA, respectively. In the case of a given text node, each row corresponds to a different sample. With the increase of text nodes, the predicted pixels are getting closer and closer to the underlying pixels, and the variance between samples gradually decreases.
Figure 5. Thompson sampling of 1-D objective function using neural process
These figures show the optimization process of 5 iterations. Each prediction function (blue) is drawn by sampling a latent variable, where the condition of the variable is to increase the number of text nodes (black). The ground truth function of the bottom layer is represented as a black dashed line. The red triangle represents the next evaluation point (evaluation point), which corresponds to the minimum value of the extracted NP curve. The red circle in the next iteration corresponds to this evaluation point, and its underlying ground truth refers to a new text node that will serve as NP.
Table 1. Bayesian optimization using Thompson sampling
The average number of optimization steps needs to reach the global minimum of the 1-D function generated by the Gaussian process. These values ​​are standardized by the number of steps taken by random search. The performance of the Gaussian process using the appropriate kernel is equivalent to the upper limit of the performance.
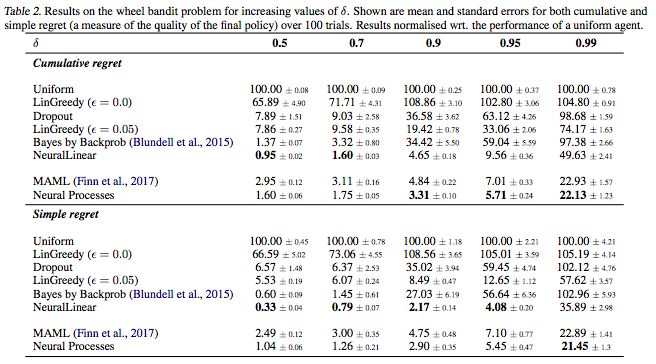
Table 2. The result of the wheel bandit problem after increasing the δ value
The result represents the average error and standard error of accumulated regret and simple regret over 100 times. The result is normalized to the performance of a uniform agent.
discuss
We introduced a set of models that combine the advantages of random processes and neural networks, called neural processes. NPs learn to express distributions as functions, and make flexible predictions based on some text input during testing. NPs do not need to write the kernel by themselves, but learn implicit measures directly from the data.
We apply NPs to a series of regression tasks to demonstrate their flexibility. The purpose of this article is to introduce NPs and compare them with ongoing research. Therefore, the task we present is that although there are many types, the dimensionality is relatively low. Extending NPs to higher dimensions may significantly reduce computational complexity and data driven representations.
Easy Electronic Technology Co.,Ltd , https://www.yxpcelectronicgroups.com