First, numpy overview
Numpy (Numerical Python) provides Python support for multidimensional array objects: ndarray, with vector computing capabilities, fast, space-saving. Numpy supports a large number of advanced dimensional arrays and matrix operations, and also provides a large library of mathematical functions for array operations.
Second, create a ndarray array
Ndarray: An N-dimensional array object (matrix), all elements must be of the same type. Ndarray attribute: ndim attribute, indicating the number of dimensions; shape attribute, indicating the size of each dimension; dtype attribute, indicating the data type.
Create an ndarray array function:

Code example:
# -*- coding: utf-8 -*- import numpy; print 'Generate a one-dimensional array using a list' data = [1,2,3,4,5,6] x = numpy.array(data) print x # Print array print x.dtype #Print array element type print 'Use list to generate 2D array' data = [[1,2],[3,4],[5,6]] x = numpy.array(data) Print x #print array print x.ndim #Print array dimensions print x.shape #Print the length of each dimension of the array. Shape is a tuple print 'Create an array using zero/ones/empty: create according to shape' x = numpy.zeros(6) #Create a one-dimensional length of 6, elements are 0 one-dimensional array print xx = numpy. Zeros((2,3)) #Create a two-dimensional 0-array with a length of 2 and a two-dimensional length of 3 print xx = numpy.ones((2,3)) #Create a one-dimensional length of 2, two-dimensional length A two-dimensional 1 array of 3 print xx = numpy.empty((3,3)) #Create a one-dimensional length of 2, a two-dimensional length of 3, an uninitialized two-dimensional array print x print 'Generate continuous elements using array' Print numpy.arange(6) # [0,1,2,3,4,5,] Open interval print numpy.arange(0,6,2) # [0, 2,4]
Third, specify the type of ndarray array elements
NumPy data type:
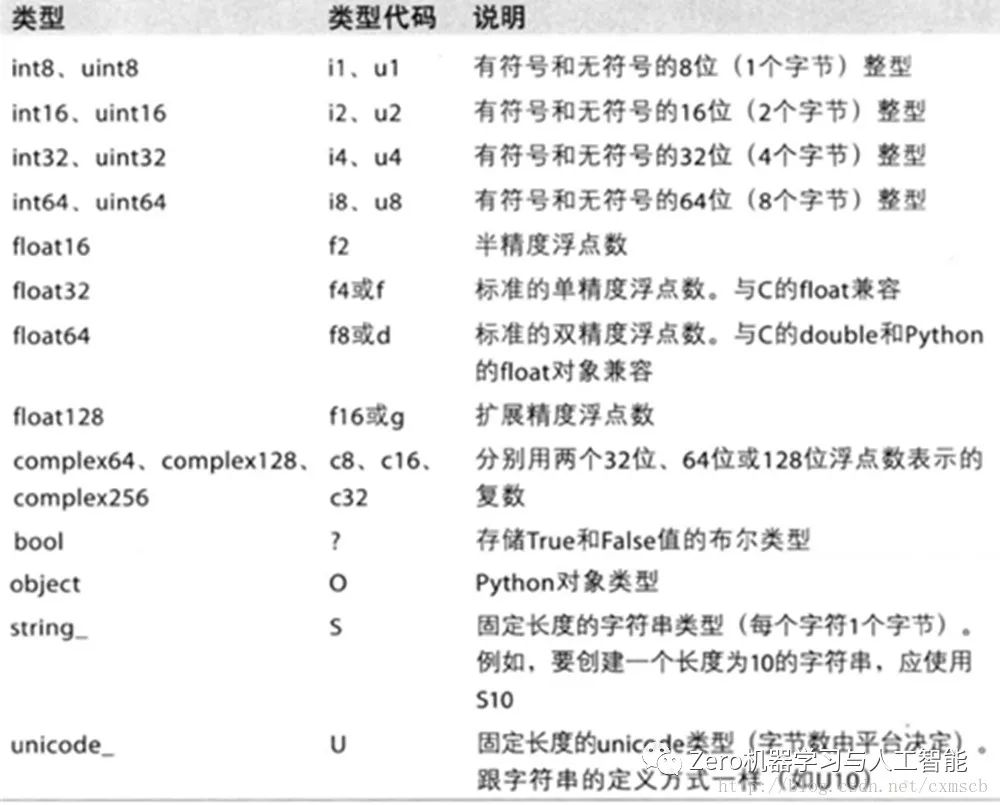
Code example:
Print 'Generate an array of the specified element type: set the dtype attribute' x = numpy.array([1,2.6,3],dtype = numpy.int64) print x # The element type is int64 print x.dtype x = numpy.array( [1,2,3],dtype = numpy.float64) print x # The element type is float64 print x.dtype print 'Use astype to copy the array and convert the type ' x = numpy.array([1,2.6,3], Dtype = numpy.float64) y = x.astype(numpy.int32) print y # [1 2 3] print x # [ 1. 2.6 3. ] z = y.astype(numpy.float64) print z # [ 1. 2. 3.] print 'convert string elements to numeric elements' x = numpy.array(['1','2','3'],dtype = numpy.string_) y = x.astype(numpy. Int32) print x # ['1' '2' '3'] print y # [1 2 3] If the conversion fails, an exception will be thrown print 'Use the data type of other array as a parameter' x = numpy.array([ 1 ., 2.6,3. ],dtype = numpy.float32); y = numpy.arange(3,dtype=numpy.int32); print y # [0 1 2] print y.astype(x.dtype) # [ 0 . 2.]
Fourth, ndarray vectorization calculation
Vector operations: operations between array keys of the same size are applied to elements. Vector and scalar operations: "broadcast" - "broadcast" scalars to individual elements
Code example:
Print 'ndarray array with scalar/array operations' x = numpy.array([1,2,3]) print x*2 # [2 4 6] print x>2 # [False False True] y = numpy.array ([3,4,5]) print x+y # [4 6 8] print x>y # [False False False]
Fifth, the basic index and slice of the ndarray array
Index of one-dimensional arrays: similar to Python's list indexing function
Index of multidimensional arrays:
Arr[r1:r2, c1:c2]
Arr[1,1] equivalent arr[1][1]
[:] data representing a dimension
Code example:
Print 'ndarray's basic index' x = numpy.array([[1,2],[3,4],[5,6]]) print x[0] # [1,2] print x[0][ 1] # 2, the index of a normal python array print x[0,1] # with x[0][1], the index of the ndarray array x = numpy.array([[[1, 2], [3,4] ], [[5, 6], [7,8]]]) print x[0] # [[1 2],[3 4]] y = x[0].copy() # Generate a copy z = x[0] # does not generate a copy print y # [[1 2],[3 4]] print y[0,0] # 1 y[0,0] = 0 z[0,0] = -1 print y # [[0 2],[3 4]] print x[0] # [[-1 2],[3 4]] print z # [[-1 2],[3 4]] print 'ndarray Slice ' x = numpy.array([1,2,3,4,5]) print x[1:3] # [2,3] Right open interval print x[:3] # [1,2,3] The default on the left is 0 print x[1:] # [2,3,4,5] The default is the number of elements on the right print x[0:4:2] # [1,3] Subscript increment 2 x = numpy.array ([[1,2],[3,4],[5,6]]) print x[:2] # [[1 2],[3 4]] print x[:2,:1] # [ [1],[3]] x[:2,:1] = 0 # Use scalar assignment print x # [[0,2],[0,4],[5,6]] x[:2,: 1] = [[8],[6]] # Assign an array with print x # [[8,2],[6,4],[5,6]]
Six, ndarray array of boolean index and fancy index
Boolean index: Use a boolean array as the index. Arr[condition], condition is a boolean array of conditions/multiple conditions.
Boolean index code example:
Print 'ndarray's boolean index' x = numpy.array([3,2,3,1,3,0]) # Boolean array must be the same length as the indexed axis y = numpy.array([True ,False,True,False,True,False]) print x[y] # [3,3,3] print x[y==False] # [2,1,0] print x>=3 # [ True False True False True False] print x[~(x>=3)] # [2,1,0] print (x==2)|(x==1) # [False True False True False False] print x[ (x==2)|(x==1)] # [2 1] x[(x==2)|(x==1)] = 0 print x # [3 0 3 0 3 0]
Fancy index: Use an integer array as an index.
Fancy index code example:
Print 'ndarray's fancy index: use an integer array as an index' x = numpy.array([1,2,3,4,5,6]) print x[[0,1,2]] # [1 2 3] print x[[-1,-2,-3]] # [6,5,4] x = numpy.array([[1,2],[3,4],[5,6]]) Print x[[0,1]] # [[1,2],[3,4]] print x[[0,1],[0,1]] # [1,4] Print x[0][ 0] and x[1][1] print x[[0,1]][:,[0,1]] # Print 01 line 01 column [[1,2],[3,4]] # Use Numpy.ix_() function enhances readability print x[numpy.ix_([0,1],[0,1])] #上上Print 01 line 01 column[[1,2],[3,4] ] x[[0,1],[0,1]] = [0,0] print x # [[0,2],[3,0],[5,6]]
Seven, ndarray array transpose and axis swap
The transpose/axis swap of an array will only return a view of the source data and will not modify the source data.
Code example:
Print 'ndarray array's transpose and axis swap ' k = numpy.arange(9) #[0,1,....8] m = k.reshape((3,3)) # Change the shape copy of the array Generate a 2-dimensional array of lengths of 3 for each dimension print k # [0 1 2 3 4 5 6 7 8] print m # [[0 1 2] [3 4 5] [6 7 8]] # Transpose (matrix) array: T attribute: mT[x][y] = m[y][x] print mT # [[0 3 6] [1 4 7] [2 5 8]] # Calculate the inner product of the matrix xTx Print numpy.dot(m,mT) # numpy.dot dot multiply #Axis object of high dimensional array k = numpy.arange(8).reshape(2,2,2) print k # [[[1 1],[ 2 3]],[[4 5],[6 7]]] print k[1][0][0] #Axis transformation transpose Parameter: tuple consisting of the axis number m = k.transpose((1, 0,2)) # m[y][x][z] = k[x][y][z] print m # [[[ 1 1],[4 5]],[[2 3],[ 6 7]]] print m[0][1][0] #axis swap swapaxes (axes: axis), argument: a pair of axis numbers m = k.swapaxes(0,1) # will the first axis and the first The two axes are exchanged m[y][x][z] = k[x][y][z] print m # [[[ 1 1],[4 5]],[[2 3],[6 7 ]]] print m[0][1][0] # Array matrix transpose using axis swap m = numpy.arange(9).reshape((3,3)) print m # [[0 1 2] [ 3 4 5] [6 7 8]] print m.swapaxes( 1,0) # [[0 3 6] [1 4 7] [2 5 8]]
Eight, ndarray universal function
A generic function (ufunc) is a function that performs element-level operations on data in ndarray.
Unary ufunc:

Unary ufunc code example:
Print 'unary ufunc example' x = numpy.arange(6) print x # [0 1 2 3 4 5] print numpy.square(x) # [ 0 1 4 9 16 25] x = numpy.array([1.5, 1.6,1.7,1.8]) y,z = numpy.modf(x) print y # [ 0.5 0.6 0.7 0.8] print z # [ 1. 1. 1. 1.]
Binary ufunc:

Binary ufunc code example:
Print 'binary ufunc example' x = numpy.array([[1,4],[6,7]]) y = numpy.array([[2,3],[5,8]]) print numpy. Maximum(x,y) # [[2,4],[6,8]] print numpy.minimum(x,y) # [[1,3],[5,7]]
Nine, NumPy where function use
Np.where(condition, x, y), the first argument is a boolean array, the second argument and the third argument can be either a scalar or an array.
Code example:
Use of print 'where function' cond = numpy.array([True,False,True,False]) x = numpy.where(cond,-2,2) print x # [-2 2 -2 2] cond = numpy .array([1,2,3,4]) x = numpy.where(cond>2,-2,2) print x # [ 2 2 -2 -2] y1 = numpy.array([-1,- 2,-3,-4]) y2 = numpy.array([1,2,3,4]) x = numpy.where(cond>2,y1,y2) #length must match print x # [1,2 , -3, -4] The nesting of the print 'where function uses ' y1 = numpy.array([-1,-2,-3,-4,-5,-6]) y2 = numpy.array([1 ,2,3,4,5,6]) y3 = numpy.zeros(6) cond = numpy.array([1,2,3,4,5,6]) x = numpy.where(cond>5, Y3,numpy.where(cond>2,y1,y2)) print x # [ 1. 2. -3. -4. -5. 0.]
Ten, ndarray commonly used statistical methods
The statistics of the entire array/an axis can be statistically calculated by these basic statistical methods.

Code example:
Print 'numpy's basic statistical method' x = numpy.array([[1,2],[3,3],[1,2]]) #Array size on the same dimension must be consistent print x.mean() # 2 print x.mean(axis=1) # average the elements of each line print x.mean(axis=0) # average the elements of each column print x.sum() #åŒç†12 print x.sum( Axis=1) # [3 6 3] print x.max() # 3 print x.max(axis=1) # [2 3 2] print x.cumsum() # [ 1 3 6 9 10 12] print x .cumprod() # [ 1 2 6 18 18 36]
Statistical method for Boolean arrays:
Sum : counts the number of True in a dimension of an array/array
Any: Stats Array/Array One or more True in a dimension
All: whether the statistics array/array is True in a dimension
Code example:
Print 'Statistical method for boolean arrays' x = numpy.array([[True,False],[True,False]]) print x.sum() # 2 print x.sum(axis=1) # [1 ,1] print x.any(axis=0) # [True,False] print x.all(axis=1) # [False,False]
Use sort to sort the dimensions of an array/array in-place (which will modify the array itself).
Code example:
Print '.sort's in-place sorting' x = numpy.array([[1,6,2],[6,1,3],[1,5,2]]) x.sort(axis=1) print x # [[1 2 6] [1 3 6] [1 2 5]] #Non-local ordering: numpy.sort() produces a copy of the array
Eleven, ndarray array deduplication and set operations

Code sample: (method return type is a one-dimensional array (1d))
Print 'ndarray's uniqueness and set operation' x = numpy.array([[1,6,2],[6,1,3],[1,5,2]]) print numpy.unique(x) # [1,2,3,5,6] y = numpy.array([1,6,5]) print numpy.in1d(x,y) # [ True True False True True False True True False] print numpy.setdiff1d (x,y) # [2 3] print numpy.intersect1d(x,y) # [1 5 6]
Twelve, linear algebra in numpy
Import numpy.linalg module. Linear algebra
Commonly used numpy.linalg module functions:

Code example:
Print 'linear algebra' import numpy.linalg as nla print 'matrix point multiplication' x = numpy.array([[1,2],[3,4]]) y = numpy.array([[1,3], [2,4]]) print x.dot(y) # [[ 5 11][11 25]] print numpy.dot(x,y) # # [[ 5 11][11 25]] print 'matrix Inverse ' x = numpy.array([[1,1],[1,2]]) y = nla.inv(x) # matrix inversion (if the inverse of the matrix exists) print x.dot(y) # unit Matrix [[ 1. 0.][ 0. 1.]] print nla.det(x) # seeking determinant
Thirteen, random number generation in numpy
Import numpy.random module.
Commonly used numpy.random module functions:

Code example:
Print 'numpy.random random number generation' import numpy.random as npr x = npr.randint(0,2,size=100000) #æ‹–å¸print (x>0).sum() # Positive result print npr.normal (size=(2,2)) #normal distribution random number array shape = (2,2)
Fourteen, ndarray array remodeling
Code example:
Print 'ndarray array remodeling' x = numpy.arange(0,6) #[0 1 2 3 4] print x #[0 1 2 3 4] print x.reshape((2,3)) # [[0 1 2][3 4 5]] print x #[0 1 2 3 4] print x.reshape((2,3)).reshape((3,2)) # [[0 1][2 3][ 4 5]] y = numpy.array([[1,1,1],[1,1,1]]) x = x.reshape(y.shape) print x # [[0 1 2][3 4 5]] print x.flatten() # [0 1 2 3 4 5] x.flatten()[0] = -1 # flatten returns a copy of print x # [[0 1 2][3 4 5]] Print x.ravel() # [0 1 2 3 4 5] x.ravel()[0] = -1 # ravel returns the view (reference) print x # [[-1 1 2][3 4 5] ] print "Dimension size is automatically derived" arr = numpy.arange(15) print arr.reshape((5, -1)) # 15 / 5 = 3
Fifteen, split and merge of ndarray arrays

Code example:
Print 'merge and split array' x = numpy.array([[1, 2, 3], [4, 5, 6]]) y = numpy.array([[7, 8, 9], [10 , 11, 12]]) print numpy.concatenate([x, y], axis = 0) # vertical combination [[ 1 2 3][ 4 5 6][ 7 8 9][10 11 12]] print numpy .concatenate([x, y], axis = 1) #水平组åˆ[[ 1 2 3 7 8 9][ 4 5 6 10 11 12]] print 'Vertical stack with horizontal stack' print numpy.vstack((x, y)) # vertical stacking: print numpy.hstack((x, y)) relative to vertical combination # horizontal stacking: relative to horizontal combination #dstack: stacking by depth numpy.split(x,2,axis=0) # Split by line[array([[1, 2, 3]]), array([[4, 5, 6]])] print numpy.split(x,3,axis=1) #分分分[array( [[1],[4]]), array([[2],[5]]), array([[3],[6]])] #Stacking aids import numpy as np arr = np.arange (6) arr1 = arr.reshape((3, 2)) arr2 = np.random.randn(3, 2) print 'r_ is used to stack by line ' print np.r_[arr1, arr2] ''' [ [ 0. 1. ] [ 2. 3. ] [ 4. 5. ] [ 0.22621904 0.39719794] [-1.2201912 -0.23623549] [-0.83229114 -0.72678578]] ''' print 'c_ is used to stack by column' print np.c_[np.r_[arr1, arr2], arr] ''' [[ 0. 1. 0. ] [ 2. 3. 1. ] [ 4. 5. 2. ] [ 0.22621904 0.39719794 3. ] [-1.2201912 -0.23623549 4. ] [-0.83229114 -0.72678578 5. ]] ''' print 'Slices directly into an array' print np.c_[1:6, -10:- 5] ''' [[ 1 -10] [ 2 -9] [ 3 -8] [ 4 -7] [ 5 -6]] '''
Sixteen, the elements of the array are repeated
Code example:
Print 'The elements of the array are repeated ' x = numpy.array([[1,2],[3,4]]) print x.repeat(2) # Repeat by element [1 1 2 2 3 3 4 4] print X.repeat(2,axis=0) # Repeat by line[[1 2][1 2][3 4][3 4]] print x.repeat(2,axis=1) # Repeat by column[[1 1 2 2][3 3 4 4]] x = numpy.array([1,2]) print numpy.tile(x,2) # tile Tile:[1 2 1 2] print numpy.tile(x, (2, 2)) # Specify the number of times to copy from low to high. # [[1 2 1 2][1 2 1 2]]
SMA means surface mount assembly. It is a new generation of electronic assembly technology, which compresses traditional electronic components into a device with a volume of only a few tenths.
Surface mounting is not a new concept, it is derived from earlier processes, such as flat mounting and mixed mounting.
For the assembly of electronic circuits, a point-to-point wiring method was initially adopted, and there was no substrate at all. The packaging of the first semiconductor device uses radial pins, which are inserted into the through holes of the monolithic circuit boards that have been used for the packaging of resistors and capacitors. Active components have been widely used in the past ten years.
Zener Diodes,Surface Mount Standard Rectifiers,Smd Bridge Rectifier,zener diodes manufacturers
Changzhou Changyuan Electronic Co., Ltd. , https://www.cydiode.com