Introduce
When a gradient descent training neural network is used, we will risk the network falling into a local minimum value. The position where the network stops on the error plane is not the lowest point of the entire plane. This is because the error plane is not inwardly convex and the plane may contain many local minima that are different from the global minimum. In addition, although in the training data, the network may reach the global minimum and converge to the desired point, we cannot guarantee how good the network learns. This means that they tend to overfit the training data.
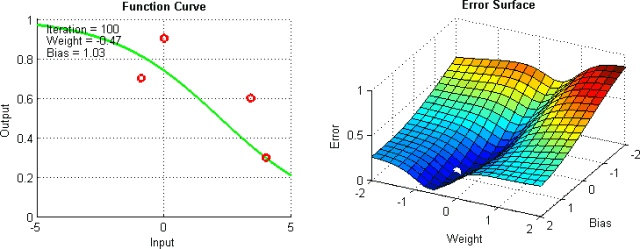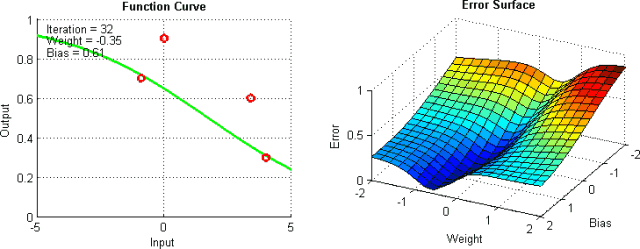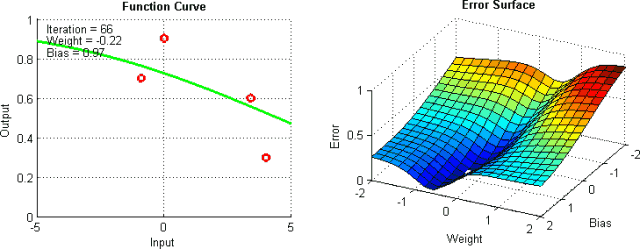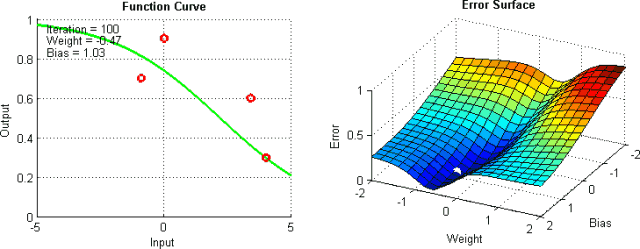
There are some means to help alleviate these problems, but there is no absolute way to prevent these problems from arising. This is because the error plane of the network is generally difficult to traverse, and the neural network as a whole is difficult to interpret.
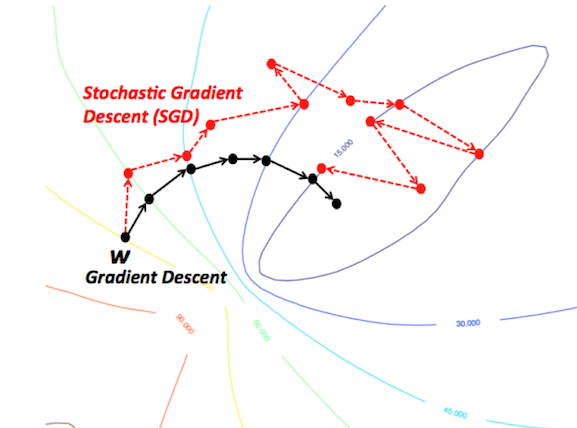
Stochastic gradient descent and mini-batch stochastic gradient descent
These algorithms adapt the standard gradient descent algorithm and use a subset of the training data in each iteration of the algorithm. SGD uses one sample per weight update and mini-batch SGD uses a predefined number of samples (usually much less than the total number of training samples). This greatly speeds up the training because we do not use the entire dataset in each iteration and it requires much less computation. At the same time, it is also expected to lead to better performance, because the intermittent movement of the network during training should allow it to better avoid local minima, while using a small part of the data set helps prevent over-fitting.
Regularization
Regularization is basically a mechanism to punish the complexity of a model by adding an item representing the complexity of the model to the loss function. In the neural network example, it punishes a larger weight, and a larger weight may mean that the neural network overfits the training data.
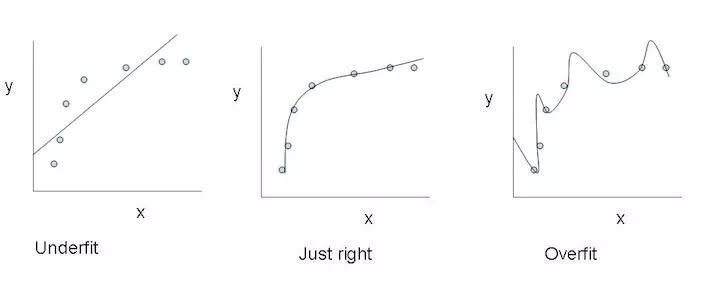
Leftmost: Underfitting; Rightmost: Overfitting
If the original loss function of the network is denoted as L(y, t) and the regularization constant is denoted as λ, after the L2 regularization is applied, the loss function is rewritten as follows:
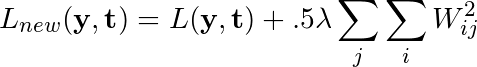
Regularization adds the sum of the squares of each weight of the network to the penalty function to punish any model with too many weights assigned to the connection, hoping to reduce the degree of overfitting.
momentum
In simple terms, momentum adds a small part of the previous weight update to the current weight update. This helps to prevent the model from falling into the local minimum, because even if the current gradient is 0, the previous gradient is not 0 in most cases, so the model is not so easy to fall into the minimum value. In addition, using momentum also makes the movement in the error plane generally smoother and moves faster.
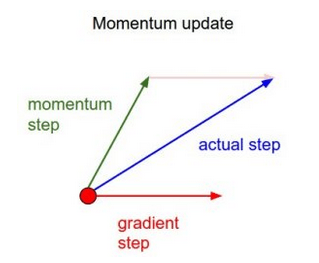
Based on this simple concept of momentum, we can rewrite the weight update equation to the following form (α is the momentum factor):
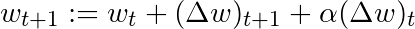
There are other more advanced forms of momentum, such as the Nesterov method.
Learning rate annealing
We may not use the same learning rate throughout the training process, but instead reduce the learning rate over time, that is, annealing.
The most common annealing plan is based on the 1/t relationship, as shown in the following figure, where T and μ0 are the given hyperparameters and μ is the current learning rate:
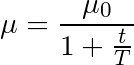
This is often referred to as a "search-then-converge" annealing plan because the network is in the "search" phase until t reaches T, and the learning rate does not drop much, after which the learning rate slows down. The network enters the "convergence" phase. This is more or less related to the balance between exploration and exploration. At the beginning, we first explored the search space and extended our overall knowledge of space. As time progressed, we transitioned to the use of the good areas we already found in the search space, shrinking to a certain minimum value.
Conclusion
These methods of improving the standard gradient descent algorithm all require the addition of hyperparameters to the model, thus increasing the time required to adjust the network. Some recently proposed new algorithms, such as Adam, Adagrad, and Adadelta, tend to optimize on a per-parameter basis rather than on global optimization, so they can fine-tune the learning rate based on individual conditions. In practice, they tend to be faster and better. The figure below also demonstrates the working process of the previously mentioned gradient descent variant. Note that more complex variants converge faster than simple momentum or SGD.
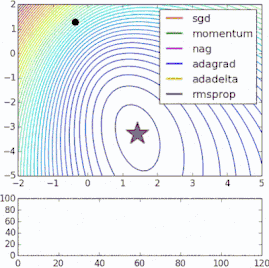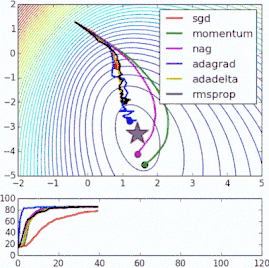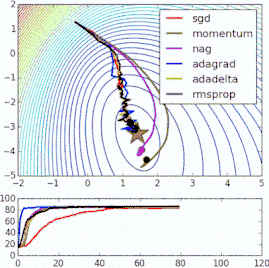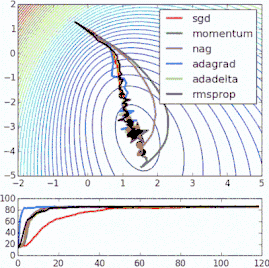
Innosilicon Machine:Innosilicon A10 ETHMaster (500Mh),Innosilicon A10 Pro ETH (500Mh),Innosilicon A10 Pro+ ETH (750Mh),Innosilicon A11 Pro ETH (1500Mh)
Innosilicon is a worldwide one-stop provider of high-speed mixed signal IPs and ASIC customization with leading market shares in Asian-Pacific market for 10 consecutive years. Its IP has enabled billions of SoC's to enter mass production, covering nodes from 180nm to 5nm across the world`s foundries including: GlobalFoundries, TSMC, Samsung, SMIC, UMC and others. Backed by its 14 years of technical expertise in developing cutting-edge IPs and ASIC products, Innosilicon has assisted our valued partners including AMD, Microchip and Microsoft to name but a few, in realizing their product goals.
Innosilicon team is fully devoted to providing the world's most advanced IP and ASIC technologies, and has achieved stellar results. In 2018, Innosilicon was the first in the world to reach mass production of the performance-leading GDDR6 interface in our cryptographic GPU product. In 2019, Innosilicon announced the availability of the HDMI v2.1 IP supporting 4K/8K displays as well as our 32Gbps SerDes PHY. In 2020, we launched the INNOLINK Chiplet which allows massive amounts of low-latency data to pass seamlessly between smaller chips as if they were all on the same bus. With a wide range of performance leading IP in multiple FinFET processes and 22nm planar processes all entering mass production, Innosilicon's remarkable innovation capabilities have been proven in fields such as: high-performance computing, high-bandwidth memory, encrypted computing, AI cloud computing, and low-power IoT.
Innosilicon Machine,A11 Pro 1500M Miner,Asic Miner A11 Pro 8G,A11 Pro 8G 1500Mh,ETC miner
Shenzhen YLHM Technology Co., Ltd. , https://www.ylhm-tech.com