Typical example of Thevenin's theorem

What is the Thevenin theorem

The Thevenin's theorem (also translated as the Thevenin's theorem), also known as the equivalent voltage source law, was an electrical theorem proposed by the French scientist L.C. Davidan in 1883. Since Helmholtz also proposed the theorem as early as 1853, it is also called the Helmholtz-Davinan theorem. The content is: a two-terminal network with an independent voltage source, an independent current source and a resistor. For its external type, an independent voltage source V and a series resistor of a relaxed two-terminal network can be electrically used. Combine to be equivalent. In a single-frequency AC system, this theorem applies not only to resistors, but also to generalized impedances. The Thevenin's theorem has important applications in the analysis of complex DC circuits with multiple power supplies and multiple circuits.

Thevenin's theorem: A linear resistor single-port network N with independent power supply. In terms of port characteristics, it can be equivalent to a single-port network with a voltage source and a resistor in series. The voltage of the voltage source is equal to the voltage uoc of the single-port network when the load is open; the resistance R0 is the equivalent resistance of the single-port network N0 obtained when all the independent power sources in the single-port network are zero.

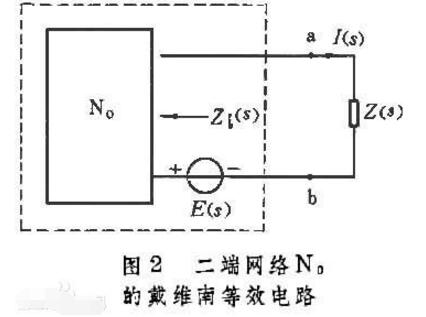
Typical example of Thevenin's theorem

The Thevenin's theorem states that the electromotive force E of the equivalent two-end network is equal to the voltage of the two-terminal network when it is open, and its series internal impedance is equal to the independent source and capacitor voltage and the inductor current in the network are zero, from the two end to the network Impedance Zi. The two-terminal network N contains independent power supply and linear time-invariant two-terminal components (resistors, inductors, capacitors). These components can be coupled, that is, there can be controlled source and mutual inductance coupling; both ends of the network N ɑ, b are connected to the load impedance Z(s), but there is no coupling between the load and the components inside the network N, U(s)=I(s)/Z(s). When all independent power supplies in network N are not working (for example, replacing the independent voltage source with a short circuit and the independent current source with an open circuit), when the initial values ​​of all capacitor voltages and inductor currents are zero, the two-terminal network can be recorded. Make N0. Thus, the current I(s) in the load impedance Z(s) can generally be calculated as in Equation 1 below (Fig. 2) where E(s) is the open circuit voltage of the network N of Figure 2, ie Z(s) Is the voltage U(s) at infinity; Zi(s) is the impedance exhibited by the two-terminal network N0; s is the complex variable introduced by the one-sided Laplace transform.

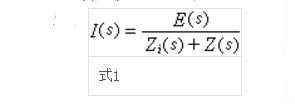
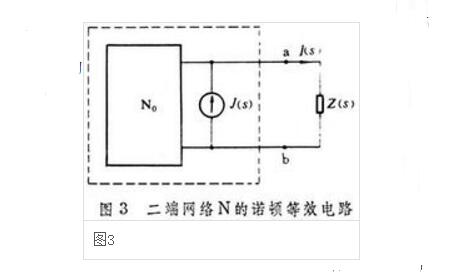
Similar to the Thevenin's theorem, there is Norton's theorem or Helmholtz-Norton's theorem. According to this theorem, any linear time-invariant two-terminal network with source can be equivalent to a two-terminal current source. Its current J is equal to the current flowing in the short-circuit line of the network. The parallel internal impedance is also equal to looking at the network. impedance. Thus, the current I(s) in Figure 1 can generally be calculated as Equation 2 below (Figure 3).

Where J(s) is the short-circuit current of the two-terminal network N of Fig. 1, that is, the current I(s) when Z(s) is equal to zero; the meaning of Zi(s) and s is the same as before.

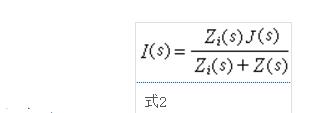
The two-end network in the dotted box of FIG. 2 and FIG. 3 is often referred to as the Thevenin equivalent circuit and the Norton equivalent circuit of the two-end network N, respectively.

Under the steady state of sinusoidal AC, Thevenin's theorem and Norton's theorem can be expressed as: When the two-terminal network N is connected to the impedance Z, the current phasor I in Z can generally be calculated according to the following formula: E, J are respectively N Open circuit voltage phasor and short circuit current phasor; Zi is the complex impedance presented by No; No is the two-terminal network N when the independent power supply is not working.

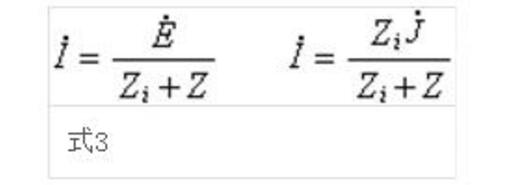
This theorem can be generalized to a two-terminal network with linear time-varying components.

Thevenin's theorem considerations

(1) The Thevenin's theorem is only equivalent to the external circuit and is not equivalent to the internal circuit. That is to say, after the theorem can not be applied to find the equivalent power electromotive force and internal resistance, it returns to the current and power of the original circuit (ie, the internal circuit of the active two-terminal network).

(2) When applying the Thevenin's theorem for analysis and calculation, if the active two-terminal network after the branch is still a complex circuit, the Thevenin theorem can be used again until it becomes a simple circuit.

(3) The Thevenin's theorem is only applicable to linear active two-terminal networks. If the active two-terminal network contains nonlinear components, the Thevenin's theorem cannot be applied.

(4) Appropriate selection of Thevenin's theorem and Norton's theorem will greatly simplify the circuit.

Applying David Nanding's comprehension questions

The problem solving steps of Thevenin's theorem:

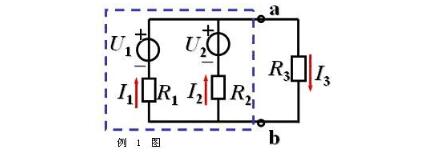
1. Divide the circuit into two parts, the branch to be sought and the active two-end network, as shown by the dotted line in Figure 1.

2. Disconnect the branch to be sought, form an active two-terminal network (to draw a picture), and find the open circuit voltage UOC of the active two-terminal network.

3. Set the power supply in the active two-terminal network to zero, retain its internal resistance (to draw), and find the equivalent resistance Rab of the network.

4. Draw the equivalent voltage source of the active two-terminal network, the voltage source voltage US=UOC (at this time pay attention to the polarity of the power supply), and the internal resistance R0=Rab.

5. Connect the branch to be sought to the equivalent voltage source and use Ohm's law to find the current.

Example 1: The circuit is shown in the figure. It is known that U1=40V, U2=20V, R1=R2=4, and R3=13. Try the Thevenin theorem to find the current I3.

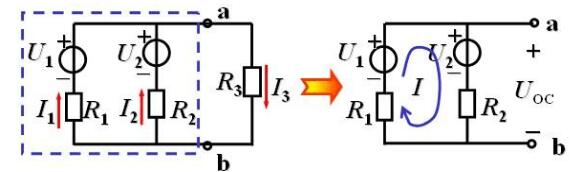
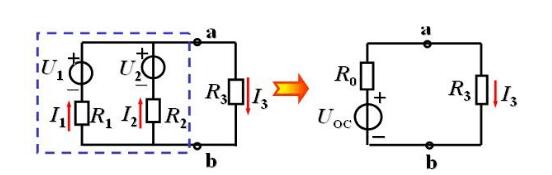
Solution: (1) Disconnect the branch to be sought for open circuit voltage UOC

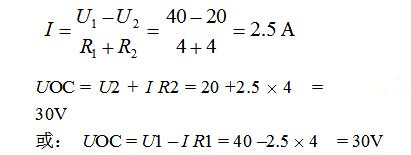
UOC can also be obtained by other methods such as the superposition principle.

(2) Find the equivalent resistance R0

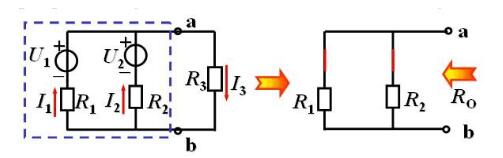
Zero all independent power supplies (ideal voltage source is replaced by short circuit, ideal current source is replaced by open circuit)

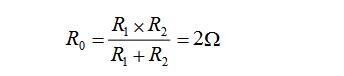
(3) Draw the equivalent circuit to find the current I3

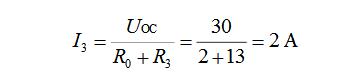
Example 2: Trying to find current I1

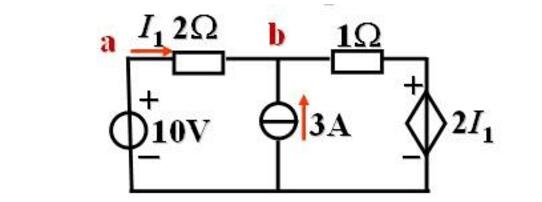
Solution: (1) Disconnect the branch to be sought for open circuit voltage UOCUOC=10 minus 3 times to 1=7V

(2) Find the equivalent resistance R0

R0=3

(3) Draw the equivalent circuit to find the current I3

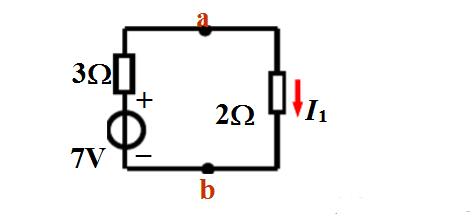
Solution: I1=1.4A

Micro Switch

✿ Material

Made of high quality plastic and metal, rust resistance and corrosion resistance, durable enough for you to hanging items, So the product appearance is exquisite, perfect workmanship.

✿ Rating

You can meet the different RATING daily needs. Please pay attention to the model of the switch before purchase, to ensure that you purchase the same as you need.

✿ Vairous Sizes

Actuator Action is momentary and Actuator Type is long straight hinge lever. Switch Body Size as shown in the picture.So different sizes can meet all your daily different needs.

✿ Wide Application

Home appliance: micro oven, electric cooker, washing machine, electric heater, warmer, water fountain and so on.

Commercial appliance: Vending machine, electric toy, electric tools, duplicating machine and so on.

Machinery: Transport machinery, printing machinery, textile machinery and so on.

Micro Switch,Micro Limit Switch,Micro Switches Types,Interruptor Micro Switch 16A 250V

Ningbo Jialin Electronics Co.,Ltd , https://www.donghai-switch.com